Conoce la eficiencia de tu algoritmo usando la notación Big O
Si te pidiera escribir una función que calcule la sumatoria de los primeros n números naturales, ¿cómo la harías?
Tal vez lo primero que se te ocurra sea lo siguiente:
function sumOf(n) {
let totalSum = 0;
for (let index = 1; index <= n; index++) {
totalSum += index;
}
return totalSum;
}Crees que hay una mejor forma de hacerlo? 🤔
function sumOf(n) {
return n * (n + 1) / 2;
}¿Cómo sabemos cuál es mejor? ¿En base a qué? ¿Tiempo de ejecución? ¿Cantidad de recursos utilizados? ¿Legibilidad del código? Quizás a simple vista parece obvio, pero de manera formal podemos saberlo.
❓ Notación O grande? (Big O Notation)
Es un método que se basa en las matemáticas (😨 calma, no te asustes) para saber como se va a comportar nuestro algoritmo, calculando un apróximado del número de operaciones a realizar (en el peor de los casos) dependiendo de la entrada de sus datos. Calculemos en los ejemplos anteriores para n = 100
// n = 100
function sumOf(n) {
// 1 operación de asignación;
let totalSum = 0;
// 1 operación de asignación;
// 1 comparación por cada iteración = 100 operaciones;
// 1 incremento por cada iteración = 100 operaciones;
// total = 201 operaciones;
for (let index = 1; index <= n; index++) {
// 1 operación de suma: totalSum + index;
// 1 operación de asignación;
// multiplicados por 100 iteraciones
// total = 200 operaciones
totalSum += index;
}
return totalSum;
}Si sumamos todas las operaciones para n = 100, sería un total de: 402 operaciones. Mientras n crece, el número de operaciones crecerá. 4 operaciones se repiten dentro del for. Y si lo definimos a través de una función matemática, el comportamiento de nuestro algoritmo sería:
f(n) = (n * 4) + 2 = 4n + 2;
Si calculamos para el segundo algoritmo:
// n = 100
function sumOf(n) {
// 1 operación de suma; 1 operación de multiplicación; 1 operación de división
return n * (n + 1) / 2;
}Para cualquier valor de n el número de operaciones siempre será la misma. A través de una función matemática: f(n) = 3; su comportamiento será constante.
La notación O Grande se escribe O( f(n) ) y se lee orden de f(n). Se usa para expresar la complejidad temporal; tiempo que tarda un algoritmo en ejecutarse. Para el primer ejemplo que vimos, estaríamos hablando de: O(4n+2) y con 4 pasos sencillos podemos definir como se comporta un algoritmo:
💀 Usa el peor caso
Si quieres hacer una búsqueda de un número dentro de un arreglo:
const numbers = [2, 8, 3, 10, 16, 30, 20, 13];
// El peor caso sería el último elemento: number = 13;
function find(number, numbers) {
for(let index = 0; index < numbers.length; index++) {
if (numbers[index] === numbers) {
return index;
}
}
}❌ Elimina las constantes
Para el caso que estudiamos anteriormente; O(4n+2) si eliminamos las constantes, nos queda: O(n)
❌ Elimina los términos insignificantes
Si tuviéramos un comportamiento en nuestro algoritmo O(3n + n^2 + 3) como n^2 es mayor a 3n entonces el comportamiento se reduce al mayor: O(n^2)
🎎 Toma en consideración todas las entradas
Para algoritmos donde tenemos varias entradas de datos, por ejemplo:
const numbers1 = [2, 8, 3, 10, 16, 30, 20, 13];
const numbers2 = [5, 9, 7, 15, 29, 43];
function doSomething(numbers1, numbers2) {
const n = numbers1.length;
const m = numbers2.length;
// O(n)
for(let i = 0; i < n; i++) {
// hace algo
}
// O(m)
for(let j = 0; j < m; j++) {
// hace algo
}
}Su comportamiento sería O(n+m).
Pensarán, «¿Tengo que pasarme la vida calculando el orden de mi algoritmo?»,
pues... si y no, con el tiempo y con práctica debería volverse algo que al ojo lo sacas.
🌅 Funciones comúnes de Notación O Grande
Existen algunas funciones comúnes con las que se suele etiquetar a los algoritmos.
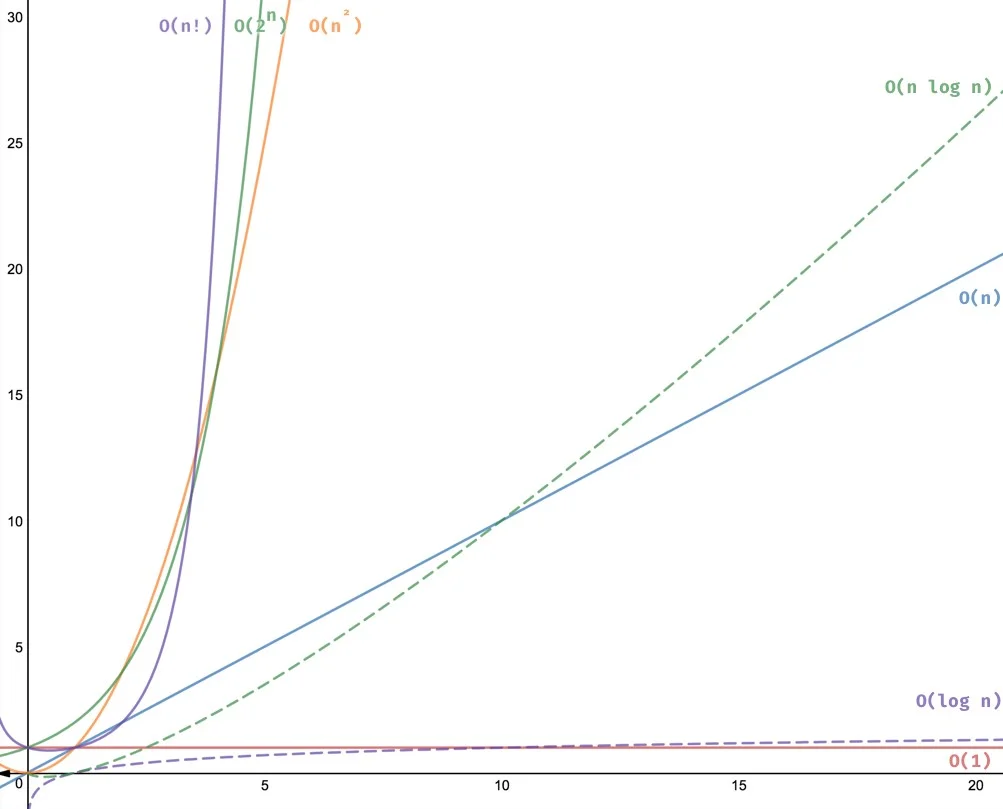
❕ Nota importante: Se mide el comportamiento de tu algoritmo. El tiempo que tarda un algoritmo en ejecutarse puede variar dependiendo del hardware que lo ejecute.
🏆 Orden uno O(1)
Si tu algoritmo es de orden 1, es lo mejor que puedes lograr, en el primer ejemplo que vimos:
// n = 100
function sumOf(n) {
// 1 operación de suma; 1 operación de multiplicación; 1 operación de división
return n * (n + 1) / 2;
}f(n) = 3 ; dado que es una constante se etiqueta como O(1).
Otro ejemplo común de orden 1 es cuando se accede a un elemento en un arreglo por su índice:
const arr = [1, 2, 3, 4, 5, ...];
// O(1) no importa si es el último elemento del arreglo
const lastElement = arr[arr.length];🏆 Orden logarítmico O(log n)
También es de lo mejor que se puede lograr, ya que si vemos el gráfico o recordamos un poco de nuestro paso por las matemáticas, a medida que crece la entrada, el número de operaciones aumenta en una proporción muy muy baja.
Algunos ejemplos de algoritmos con esta característica y que veremos más adelante es Búsqueda binaria.
🏅 Orden lineal O(n)
Es muy común y fácil de detectar, por ejemplo:
// Imprimir todos los elementos de un arreglo
const arr = [1, 2, 3, 4, 5, ...];
function printAllElements(arr) {
for (let i = 0; i < arr.length; i++) {
console.log(arr[i]);
}
}
printAllElements(arr);😌 Orden n-logarítmico O(n log n)
Lo veremos más adelante. Algunos de los algoritmos más comúnes que son etiquetados con este orden son: Ordenamiento por mezcla y Divide y vencerás.
🧐 Orden polinómico o cuadrático O(n log n)
Son algoritmos comúnes pero cuando te encuentras con ellos es bueno revisarlo a ver si se puede mejorar, por ejemplo:
const words = [ "hello", "how" , "are", "you", "Mr.", "Jones", "how", "you", "doing" , ...];
// ciclo anidado
function hasDuplicates(words) {
for (let i = 0; i < words.length; i++) {
for (let j = 0; j <words.length; j++)
if (i === j) continue;
if (words[i] === words[j]) {
return true;
}
}
}
return false;
}Si calculamos el orden de este algoritmo sería: O(n^2). Pero se puede mejorar usando un Map, veamos:
const words = [ "hello", "how" , "are", "you", "Mr.", "Jones", "how", "you", "doing" , ...];
function hasDuplicates(words) {
let dictionary = new Map();
for (let i = 0; i < words.length; i++) {
if (dictionary.get(words[i]) === undefined) {
//insertamos la palabra
dictionary.set(words[i], 1);
} else {
//existe la palabra, ya hay una duplicada
return true;
}
}
return false;
}En el peor de los casos, este algoritmo es de O(n).
💀 Orden exponencial O(2^n) y factorial O(n!)
Son casos que definitivamente se van a tardar ⌚, debemos ser cuidadosos. Comúnmente hacen permutaciones de la entrada de tus datos, un ejemplo de permutación sería:
Usando Recursión aquí mi otro post.
const word = "abc";
function permute(word) {
if (word.length < 2 ){
return words
}
let permutationsArray = [];
for (let i = 0; i < word.length; i++){
let char = word[i];
let remainingChars = word.slice(0, i) + word.slice(i + 1, word.length)
for (let permutation of permute(remainingChars)) {
permutationsArray.push(char + permutation);
}
}
return permutationsArray;
}
permute(word) // [ 'abc', 'acb', 'bac', 'bca', 'cab', 'cba' ]👀 Comparación entre O(1) y O(n)
Con el primer ejemplo que vimos, veamos un gráfico de ambos algoritmos para los valores; n = 5000, 50000, 500000, 5000000, 50000000. Usando la herramienta Performance Tracker podemos ver el comportamiento de ambos algoritmos.
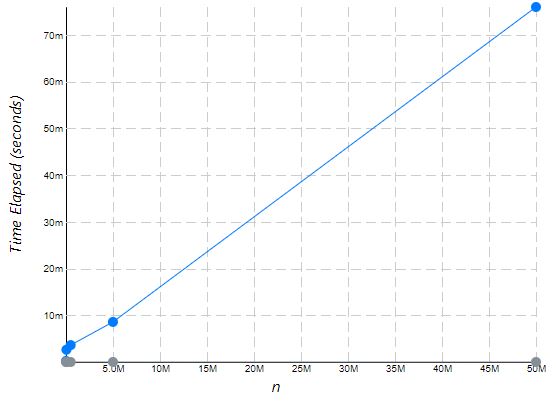
Por cierto, el primer ejemplo que vimos se trata de Número triangular
🧠 Complejidad espacial
Se ha hablado del número de operaciones o tiempo que toma un algoritmo para ejecutarse en base a la entrada de sus datos. Pero también existe la Complejidad espacial que debemos considerar. Se enfoca en el uso de la memoria y se representa con la misma notación. Por ejemplo, en un caso anterior que usamos un Map como estructura auxiliar, estaríamos hablando de una complejidad espacial de O(n) para que la complejidad temporal de nuestro algoritmo sea de O(n). Otro caso común son los algoritmos de ordenación que usan estructuras auxiliares para reordenar los elementos.
📝 Conclusiones
La eficiencia de los algoritmos que creamos es algo que siempre debemos considerar. Recuerda usar el peor caso, eliminar las constantes y los términos menos dominantes O(3n^2 + 10n = n^2). Los ciclos anidados deben re-evaluarse. Dependiendo de la cantidad de datos que estemos manuipulando nos podemos ahorrar una gran cantidad de tiempo de computo.
Y por último les dejo una cita de C. A. R. Hoare:
«Hay dos maneras de diseñar software: una es hacerlo tan simple que sea obvia su falta de deficiencias, y la otra es hacerlo tan complejo que no haya deficiencias obvias»