Una breve historia de dragones, recursión y memoization
"Para entender la recursión primero debemos entender la recursión"
anónimo
👦 Martin y el Dragón 🐲
En tiempos antiguos, antes de que los computadores fueran inventados, alquimistas estudiaron las propiedades míticas de los números. Como no había computadores, tenían que acudir a dragones para hacer el trabajo. Los dragones eran bestias inteligentes pero también perezosos y malhumorados.
Un día un alquimista le dio a Martin una lista de números y lo envió a una cueva para que le preguntase al dragón si alguno de esos números era impar. Martin no había estado en la cueva antes, así que tomó una vela y fue entrando tímidamente y con cuidado hasta encontrar en el fondo a un viejo dragón.

"Que quieres?" -gruñó el dragón mientras lo miraba con sospecha-
"Por favor, dragón tengo una lista de números y necesito saber si alguno es impar" -dijo Martin-
"Aquí está" -escribió la lista en el suelo con su dedo-
(3142, 5798, 6550, 8914)
"Lo siento chico" -dijo el dragón, en tono malhumorado y continuó...-
"Podría estar dipuesto a decirte si el primero de esa lista es impar, pero es lo mejor que puedo hacer"
"Pero necesito saber si algún número de la lista es impar, no solo el primero" -le explicó Martin-
"Qué lástima por tí!" -y el dragón continuó...-
"Solo voy a mirar el primero de la lista. Pero puedo mirar todas las listas que quieras, una a la vez" -Martin pensó por un momento. Tenía que haber una forma de evitar el mal humor.
"Qué tal esta lista?" -preguntó señalando la que había dibujado en el suelo-
(3142, 5798, 6550, 8914)
"El primer número de la lista no es impar" -dijo el dragón-
-Luego Martin cubrió el primer elemento de la lista con su mano y dibujó un nuevo paréntesis quedando:
(5798, 6550, 8914) "Y ahora esta lista?"
"El primer número de la lista no es impar" -respondió el dragón-
-Martin hizo el mismo proceso, quedando:
(6550, 8914)
"El primer número de la lista tampoco es impar" -repitió el dragón-
-repitió el proceso hasta quedar:
()
"Esa es una lista vacía, no puede haber un número impar porque no hay nada allí" -volvió el dragón-
"Bien, ahora sé que no hay ningún número impar en la lista, todos son par" -exclamó Martin-
"Yo NUNCA dije eso!!" -gritó el dragón-
-Y Martin dibujó todas las listas que le preguntó al dragón-
(3142, 5798, 6550, 8914)
(5798, 6550, 8914)
(6550, 8914)
(8914)
()
"No lo ves? diciéndome que el primer elemento de cada lista no es impar, entonces ninguno de mi lista es impar." -preguntó Martin-
"Eso es bastante complicado, parece que has descubierto la recursión, pero no me preguntes qué significa, tendrás que descubrirlo por tu cuenta." -finalizó el dragón-Nota: historia extraída tal cual del libro Common LISP: A Gentle Introduction to Symbolic Computation
🔄 Recursión
Seguramente sepas que en la historia anterior, podemos hacer un ciclo e iterar la lista y preguntar por cada elemento si es impar hasta llegar al final de la lista. A través de la Recursión podemos hacer exactamente lo mismo pero de una forma diferente llamándonos a sí mismos (en este caso a una función).
Veamos la conversación de Martin y el Dragon usando JavaScript:
function isOdd( number ) {
return number % 2 != 0;
}
function isAnyOddNumberIn( numbers ) {
// caso base
if (numbers.length === 0) {
return false;
}
// obtenemos primer elemento y el resto en 2 variables
let [firstNumber, ...rest] = numbers;
// preguntamos si es impar el primer elemento
if (isOdd( firstNumber )) {
return true;
}
// si no es impar, volvemos a preguntar con el resto de la lista
return isAnyOddNumberIn( rest );
}
let numbers = [3142, 5798, 6550, 8914];
console.log(isAnyOddNumberIn( numbers )); // false🚧 Caso Base
Saber cuando detenerse. Lo primero que podemos ver en la función isAnyOddNumberIn(numbers) es que hay un caso base, preguntamos si la lista está vacía, es la forma en la que finalizamos la recursión. Siempre debe haber un caso base sino queremos que suceda un error o tener un resultado inesperado.
🕵 Los argumentos
La idea es que en cada iteración nuestro problema sea cada vez más pequeño. En este caso tenemos un sólo argumento que es la lista de números, en cada llamada la lista es más pequeña. Si no disminuimos la lista o utilizamos siempre la misma, entrará en un ciclo infinito y ocasionará eventualmente el famoso Stack Overflow.
🚑 Contexto de ejecución y Stack
La información acerca de la ejecución de una función es almacenada en un contexto de ejecución. Es una estructura de datos que contiene los detalles de la ejecución de una función, tales como: qué instrucción se está ejecutando, las variables, etc.
En cada llamada se pausa la ejecución actual y se apila en un Stack el contexto actual. La mayoría de los lenguajes usan un Call Stack para almacenar los contextos de ejecución y colocan un límite para evitar un Stack Overflow.
🌎 El camino más largo en una pirámide
/5/
/4/ 3
/7/ 9 7
/9/ 7 6 5
/8/ 2 4 8 6Este es un problema que se puede hacer con recursión. Haciendo un análisis, podemos hacer un recorrido hacia abajo, hasta llegar a la base de la pirámide luego desde abajo ir sumando y verificando la suma o elemento máximo de cada lado dependiendo de la posición en la que estemos.
Si nos posicionamos en el primer escalón, en cada posición de la pirámide y sumamos con el máximo entre el lado izquierdo y derecho, veremos:
-> (9) (7) (6) (5) = 17 11 14 13
8/ 2 \4 \8/ 6Nota: del lado derecho calculamos la suma acumulada en la posición respectiva eligiendo el máximo de cada lado.
Y si subimos al otro escalón quedaría:
-> (7) (9) (7) = 24 23 21
9/ 7 \6/ 5
8/ 2 4 \8 6nuevamente:
-> (4) (3) = 28 26
7/ 9/ 7
9/ 7 \6 5
8/ 2 4 \8 6Y finalmenente:
-> /5/ = 33
/4/ 3
/7/ 9 7
/9/ 7 6 5
/8/ 2 4 8 6Si vemos la solución de este algoritmo:
function maxPathWeight( pyramid, floor, position ) {
let currentNode = pyramid[floor][position];
// cuando llegamos a la base de la piramide, retornamos
// para acumularlo
if (floor === pyramid.length - 1) {
return currentNode;
}
// calculamos el acumulado del lado izquierdo hacia abajo
let leftPath = currentNode + maxPathWeight(pyramid, floor + 1, position);
// calculamos el acumulado del lado derecho hacia abajo
let rightPath = currentNode + maxPathWeight(pyramid, floor + 1, position + 1);
// retornamos el máximo de los caminos
return Math.max(leftPath, rightPath);
}
function longestPath( pyramid ) {
// comenzamos desde la raíz la posición [0][0]
return maxPathWeight(pyramid, 0, 0);
}
let pyramid =
[
[5],
[4, 3],
[7, 9, 7],
[9, 7, 6, 5],
[8, 2, 4, 8, 6]];
console.log( longestPath( pyramid ) ); // 33🚀 Memoization
También conocido como Programación dinámica, es una técnica utilizada para optimizar soluciones a problemas que se pueden dividir en sub-problemas, usualmente usando recursión. Y la idea principal es que una vez que resolvamos un sub-problema almacenamos el resultado, de manera que si lo necesitamos nuevamente ya tenemos el resultado almacenado. Estoy seguro que eso se les parece a un concepto ya conocido 🤔 sí, a una caché.
Veamos el problema del ejercicio anterior
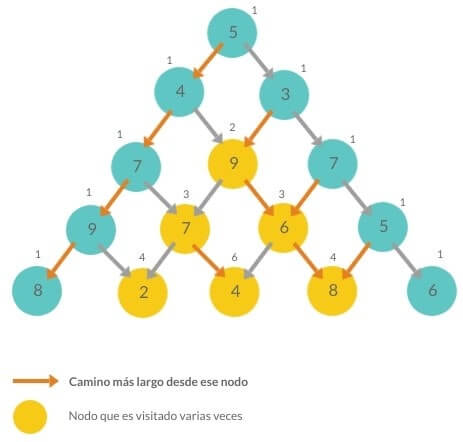
Si vemos cada posición del array como un nodo, podemos ver cuántas veces es visitado cada nodo para poder obtener el camino más largo, lo cual no es eficiente si ya sabemos al posicionarnos en un nodo cuál es el camino más largo hacia abajo a partir de él, entonces usemos una caché.
Nota: para este caso en particular quizás no se nota tanto la diferencia. pero si intentamos ejecutar el mismo algoritmo con una pirámide más grande, ⏳ seguramente no culmine.
pero lo podemos optimizar para que cada nodo no tenga que hacer el mismo procesamiento más de una vez y nuestra solución sea óptima. Veamos en el siguiente código:
// creamos una cache
const cache = new Map();
function maxPathWeight( pyramid, floor, position ) {
let currentNode = pyramid[floor][position];
// cuando llegamos a la base de la piramide, retornamos
// para acumularlo
if (floor === pyramid.length - 1) {
return currentNode;
}
// creamos una key, ejemplo: '2,1'
let key = floor + ',' + position;
// si el nodo ya ha sido visitado, retornamos su valor
if (cache.get(key) !== undefined) {
return cache.get(key);
}
// sino calculamos el acumulado del lado izquierdo hacia abajo
let leftPath = currentNode + maxPathWeight(pyramid, floor + 1, position);
// y calculamos el acumulado del lado derecho hacia abajo
let rightPath = currentNode + maxPathWeight(pyramid, floor + 1, position + 1);
// lo guardamos en caché
cache.set(key, Math.max(leftPath, rightPath));
// retornamos el máximo de los caminos
return Math.max(leftPath, rightPath);
}
function longestPath( pyramid ) {
// comenzamos desde la raíz la posición [0][0]
return maxPathWeight(pyramid, 0, 0);
}
let pyramid =
[
[5],
[4, 3],
[7, 9, 7],
[9, 7, 6, 5],
[8, 2, 4, 8, 6]];
console.log( longestPath( pyramid ) ); // 33Ahora si quieres ejecutarlo acá el código pirámide más grande usando memoization verás el resultado de manera instantánea.
📝 Conclusiones
Cuando abordamos una solución recursiva debemos tener en cuenta:
- Caso base o condición de parada.
- Cada llamada debe hacer el problema más pequeño.
La programación dinámica o memoization nos puede ayudar a optimizar una solución recursiva utilizando algo que ya conocemos, una caché.
La recursión también se encuentra en el arte y la literatura, por ejemplo Las mil y una noches o Las muñecas rusas.
Y por último les dejo una frase atribuida al emperador romano:
«Divide y vencerás»
Julio César